목차
2022-02-18
실험실에서 진행하는 프로젝트에서 2D 이미지 내에서 카메라와 물체까지의 3차원 거리를 구하는 task가 주어졌다.
기하학적 계산에 앞서 2차원 이미지의 3차원 변환을 위해서는 camera의 내부 파라미터정보가 필요하기 때문에
카메라 캘리브레이션 과정을 통해 카메라 내부 파라미터를 구하는 과정을 정리하고자 한다.
카메라 캘리브레이션은 영상처리, 컴퓨터비전 분야에서 필수적인 과정이다.
이번 글에서는 카메라 캘리브레이션의 기본적인 개념, 카메라 내부 파라미터 정보를 얻기 위한 Tool과 획득과정등을 정리해보았다.

0. 카메라 캘리브레이션이란?
우리가 눈으로 보는 실제 세상은 3차원이다. 하지만 이것을 단안렌즈 카메라로 촬영하면 2차원의 이미지로 투영된다. 이때 3차원의 점들이 이미지 상에서 어디에 맺히는지는 기하학적으로 생각하면 영상을 찍을 당시의 카메라의 위치, 방향에 따라 바뀔것이다. 하지만 실제 이미지는 사용된 렌즈, 렌즈와 이미지 센서와의 거리, 렌즈와 이미지 센서가 이루는 각 등 카메라 내부의 기구적인 부분에 의해서도 크게 영향을 받는다.
따라서 3차원 점들이 2차원 영상에 투영된 위치를 구하거나, 역으로 2차원 영상좌표로부터 3차원 공간좌표를 구하고자 할 때는 이러한 내부 요인(방해 요인)들을 제거해야 정확한 계산이 가능하다. 이러한 내부 요인의 파라미터 값들을 구하는 과정을 카메라 캘리브레이션이라 한다.
1. 카메라 내부 파라미터
구하고자 하는 내부 파라미터는 다음과 같다.
- 초점거리(focal length): Fx, Fy
- 주점(principle point): Cx, Cy
- 비대칭계수(screw coefficient): screw_c = tanα
a. 초점거리(focal length)
: 렌즈 중심과 이미지센서(CCD, CMOS 등)와의 거리
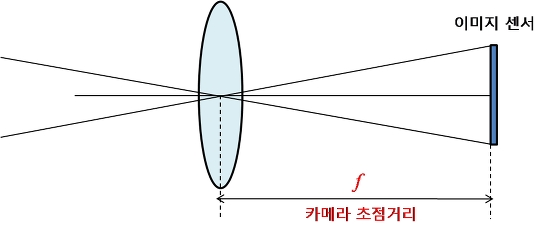
디지털 카메라 등에서 초점거리는 mm 단위로 표현되지만 카메라 모델에서 말하는 초점거리(f)는 픽셀(pixel) 단위로 표현된다. 즉, f의 단위로 픽셀이라는 의미한다.
이미지의 픽셀(pixel)은 이미지 센서의 셀(cell)에 대응되기 때문에, 초점거리(f)가 픽셀(pixel) 단위라는 의미는 초점거리가 이미지 센서의 셀(cell) 크기에 대한 상대적인 값으로 표현된다는 의미입니다. 예를 들어, 이미지 센서의 셀(cell)의 크기가 0.1 mm이고 카메라의 초점거리가 f = 500 pixel이라고 하면 이 카메라의 렌즈 중심에서 이미지 센서까지의 거리는 이미지 센서 셀(cell) 크기의 500배 즉, 50 mm라는 의미입니다.
컴퓨터 비전 분야에서 카메라 초점거리를 물리단위(m, cm, mm, ...)가 아닌 픽셀단위로 표현하는 이유는 (이미지 픽셀과 동일한 단위로 초점거리를 표현함으로써) 영상에서의 기하학적 해석을 용이하게 하기 위함입니다.
그런데, 카메라 모델에서 초점거리를 하나의 값으로 f라 표현하지 않고 fx, fy로 구분하여 표현하는 경우가 있는데(실제로 카메라 캘리브레이션을 수행하면 fx, fy를 구분하여 반환한다) 이는 이미지 센서의 물리적인 셀 간격이 가로 방향과 세로 방향이 서로 다를 수 있음을 모델링하기 위함입니다. 이 경우 fx는 초점거리(렌즈중심에서 이미지 센서까지의 거리)가 가로 방향 셀 크기(간격)의 몇 배인지를 나타내고 fy는 초점거리가 세로 방향 센서 셀 크기(간격)의 몇 배인지를 나타냅니다. fx와 fy 모두 단위는 픽셀(pixel)이며 현대의 일반적인 카메라는 가로방향 셀 간격과 세로방향 셀 간격의 차이가 없기 때문에 f = fx = fy라 놓아도 무방합니다.
참고로, 동일한 카메라로 캘리브레이션을 수행했을 때, 이미지 해상도를 1/2로 낮추면 캘리브레이션 결과의 초점거리도 1/2로 작아집니다. 실제 물리적 초점거리가 변하는 것은 아니지만 카메라 모델에서의 초점거리는 상대적인 개념이기 때문에 해상도를 바꾸면 한 픽셀(pixel)에 대응하는 물리크기가 변하고 따라서 초점거리도 변하게 됩니다. 예컨데, 이미지 해상도를 1/2로 낮추면 이미지 센서의 2 x 2 셀(cell)들이 합쳐서 하나의 이미지 픽셀이 되기 때문에 한 픽셀에 대응하는 물리크기가 2배가 됩니다. 따라서 초점거리는 1/2이 되어야 합니다.
카메라 모델의 렌즈중심(초점)은 핀홀 카메라 모델(그림 6)에서 핀홀(pinhole)에 해당됩니다. 핀홀 카메라 모델은 모든 빛은 한 점(초점)을 직선으로 통과하여 이미지 평면(센서)에 투영된다는 모델입니다. 이러한 핀홀 모델은 3D 공간과 2D 이미지 평면 사이의 기하학적 투영(projection) 관계를 매우 단순화시켜 줍니다.
초점으로부터 거리가 1(unit distance)인 평면을 normalized image plane이라고 부르며 이 평면상의 좌표를 보통 normalized image coordinate라고 부릅니다. 물론 이것은 실제는 존재하지 않는 가상의(상상의) 이미지 평면입니다. 카메라 좌표계 상의 한 점 (Xc, Yc, Zc)를 영상좌표계로 변환할 때 먼저 Xc, Yc를 Zc(카메라 초점에서의 거리)로 나누는 것은 이 normalized image plane 상의 좌표로 변환하는 것이며, 여기에 다시 초점거리 f를 곱하면 우리가 원하는 이미지 평면에서의 영상좌표(pixel)가 나옵니다 (그림 4 참조). 그런데, 이미지에서 픽셀좌표는 이미지의 중심이 아닌 이미지의 좌상단 모서리를 기준(원점)으로 하기 때문에 실제 최종적인 영상좌표는 여기에 (cx, cy)를 더한 값이 됩니다. 즉, x = fxX/Z+cx, y = fyY/Z+cy. 카메라 모델에서 사용하는 좌표계 표현 및 변환에 대한 보다 자세한 내용에 대해서는 [영상처리] - [영상 Geometry #1] 좌표계 글을 참조하기 바랍니다.
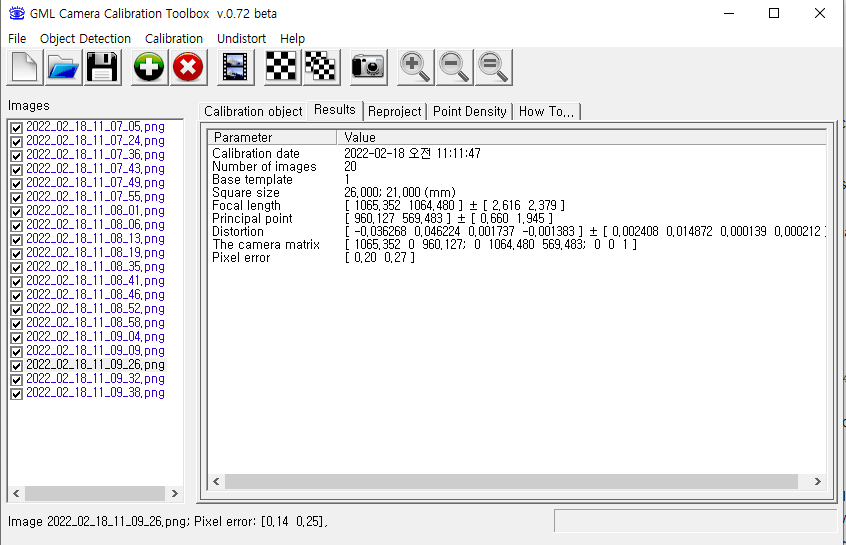
Focal length = fx, fy
principle point = cx, cy
Distortion = k1, k2, p1, p2
reference
'카메라 > 기하학' 카테고리의 다른 글
| [Depth camera] 이론 (0) | 2022.04.25 |
|---|---|
| 2D 영상에서 물체까지 3D 거리 구하기 (5) | 2022.02.19 |
| 카메라의 위치 및 3D 자세정보 (2) | 2022.02.18 |
| 카메라 왜곡보정 - Camera Models (0) | 2021.06.27 |